|
|

Un trader d’options peut donc éprouver le besoin d’estimer quel serait son nouveau delta, et donc quelle serait la nouvelle valeur de son option, si le prix du sous-jacent augmentait ou diminuait de tant. Pour ce faire, il peut s’aider du gamma de son option ou de sa position.
Comme nous allons voir, le gamma mesure précisément la variabilité du delta. Si vous cherchez un courtier pour investir dans les options, cliquez ici.
Gamma Options
Définition
Le gamma d’une option
Qu’est-ce que le gamma ? Le gamma est la mesure dans laquelle le delta d’une option augmente/diminue quand le prix du sous-jacent augmente/diminue.
La valeur du gamma est généralement exprimé sous la forme d’un nombre positif. Il s’agit du nombre de deltas qu’il faudrait ajouter ou soustraire à l’ancien delta si le prix du sous-jacent augmentait ou diminuait de un point. Si le prix du sous-jacent augmente de un point, il faut ajouter le montant du gamma à l’ancien delta ; si le prix du sous-jacent diminue de un point, il faut soustraire le montant du gamma à l’ancien delta. Par exemple, si le gamma d’un call s’élève à 1 (0,01 dans le format décimal), le delta de l’option doit augmenter de 1 (0,01) point si le prix du sous-jacent augmente de un point. Et le delta de l’option doit diminuer de 1 (0,01) point si le prix du sous-jacent diminue de un point.
Exemples

Prenons l’exemple du call de strike 7,7 ci-dessus. Il est à la monnaie, et il a un delta de 51 (0,51 dans le format décimal), un gamma de 38 (0,38 dans le format décimal). Si le prix du sous-jacent augmente de 1 point, le nouveau delta de l’option s’élèvera à 89 (0,89 dans le format décimal). Si le prix du sous-jacent diminue de 1 point, le nouveau delta de l’option s’élèvera à 13 (0,13 dans le format décimal). Prenons maintenant le cas d’un put à la monnaie dont le delta est -47 (-0,47 dans le format décimal) et dont le gamma est 1 (0,01 dans le format décimal). Si le prix du sous-jacent augmente de 1 point, le nouveau delta s’élèvera à -46 (-0,46 dans le format décimal). Si le prix du sous-jacent diminue de 1 point, le nouveau delta s’élèvera à -48 (-0,48 dans le format décimal).
Le gamma d’une position
Le gamma d’un call ou d’un put est toujours positif. Mais il n’en va pas de même du gamma d’une position. Lorsqu’un trader a une position acheteuse, le gamma de la position longue est positif, quelle que soit la nature des options impliquées (des calls ou des puts). Lorsqu’un trader a une position vendeuse, le gamma de la position courte est négatif, quelle que soit la nature des options impliquées. Par exemple, le gamma d’une position short put se présente sous la forme d’un nombre négatif.
Une position dont le gamma est positif voit son delta augmenter lorsque le prix du sous-jacent augmente. Puisqu’on ajoute alors un nombre positif (le gamma) à l’ancien delta. En revanche, elle voit son delta diminuer lorsque le prix du sous-jacent diminue. Puisqu’on soustrait alors un nombre positif (le gamma) à l’ancien delta. À l’inverse, une position dont le gamma est négatif voit son delta diminuer lorsque le prix du sous-jacent augmente. Puisqu’on ajoute alors un nombre négatif (le gamma) à l’ancien delta. En revanche, elle voit son delta augmenter lorsque le prix du sous-jacent diminue. Puisqu’on soustrait alors un nombre négatif (le gamma) à l’ancien delta.
L’ami des acheteurs, l’ennemi des vendeurs
Cela signifie que le gamma est l’ami des acheteurs. En effet, il permet à une position longue d’empocher plus d’argent à chaque fois que le prix du sous-jacent évolue en notre faveur. Et il lui permet de perdre moins d’argent à chaque fois que le prix du sous-jacent évolue en notre défaveur. Prenons l’exemple d’un call long dont le delta est positif (+56). Il s’agit donc d’une position haussière. Et son gamma s’élève à +5. Si le prix du sous-jacent augmente et évolue en notre faveur, il faudra ajouter le gamma de la position (+5) à l’ancien delta (+56). La position présentera alors un delta de +61. Si bien qu’elle empochera non plus 56 $ mais 61 $ à chaque fois que le sous-jacent évoluera en notre faveur (à la hausse) de un point.
Si le prix du sous-jacent diminue et évolue en notre défaveur, il faudra soustraire le gamma de la position (+5) à l’ancien delta (+56). La position présentera alors un delta de +51. Si bien qu’elle perdra non plus 56 $ mais seulement 51 $ à chaque fois que le sous-jacent évoluera en notre défaveur (à la baisse) de un point.
S’il est l’ami des acheteurs, le gamma est l’ennemi des vendeurs. Le gamma négatif des positions courtes fait que celles-ci gagnent moins d’argent à chaque fois que le prix du sous-jacent évolue en notre faveur. Et qu’elles perdent plus d’argent à chaque fois que le prix du sous-jacent évolue en notre défaveur.
Les fluctuations du gamma. Le risque gamma.
Fluctuations du gamma
Dans un cycle d’expiration donné, le gamma le plus élevé est celui des options à la monnaie. Dans le cycle ci-dessous, on peut voir que gamma du call et du put à la monnaie (de strike 382) est le plus élevé de tous. Et, à mesure qu’on s’éloigne de ce strike dans la monnaie ou hors de la monnaie, le gamma diminue.
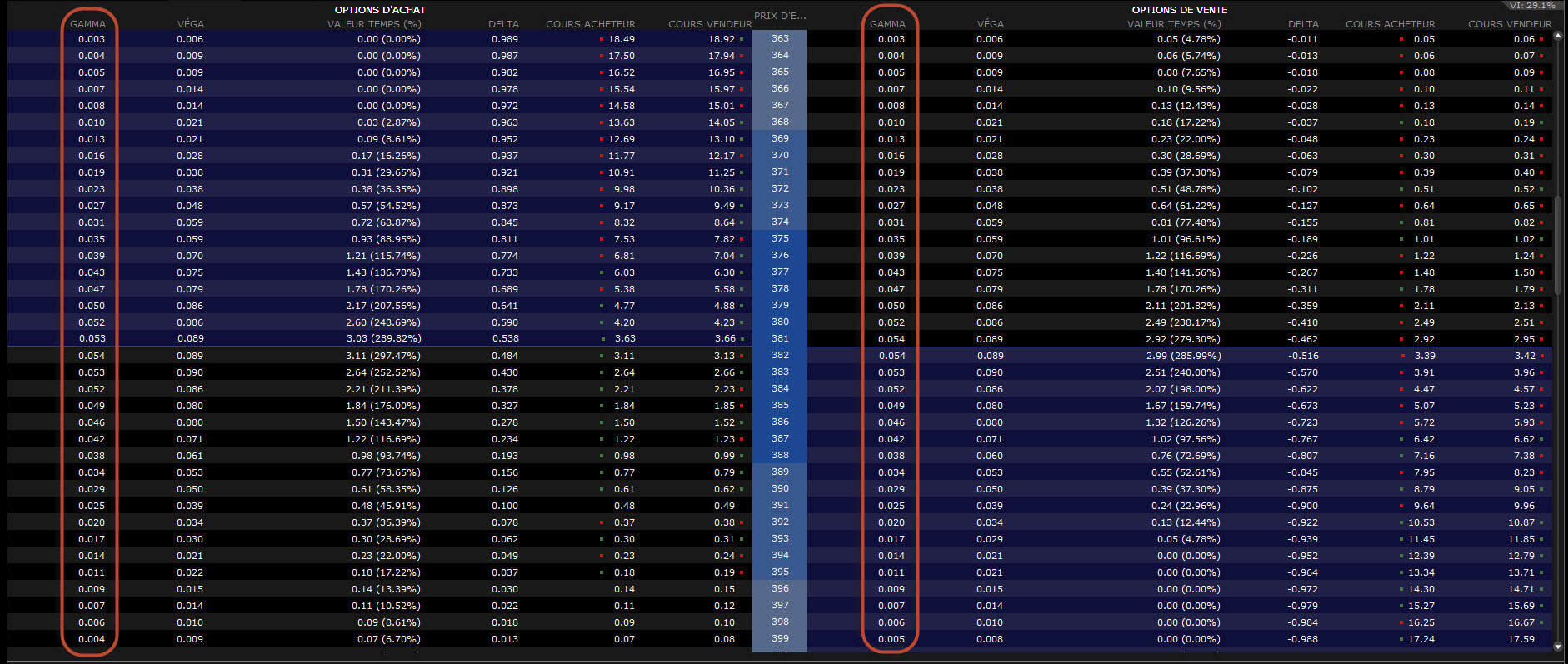
La valeur du gamma d’une option ne dépend pas seulement de son rapport au strike à la monnaie. Le gamma dépend du nombre de jours restant avant l’échéance et de la volatilité du marché sous-jacent. Le gamma d’une option à la monnaie augmente si le nombre de jours restants ou si la volatilité diminue. Et le gamma d’une option à la monnaie diminue si on augmente le nombre de jours restants ou la volatilité. Dans la figure ci-dessous, on peut voir que la courbe du gamma correspondant à moins de jours et moins de volatilité (petits pointillés) est plus haute que les deux autres courbes.
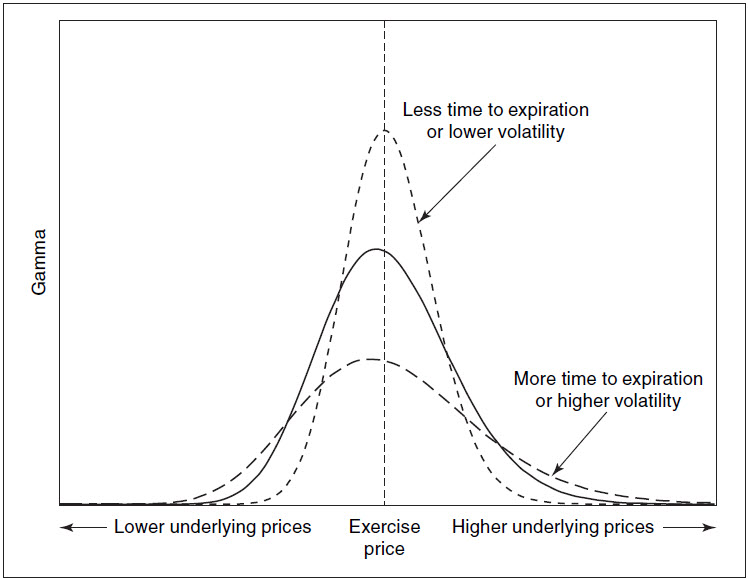
Le risque gamma
Le gamma est à son maximum chez les options à la monnaie. Et le gamma d’une option à la monnaie augmente avec le passage du temps ou la baisse de la volatilité. Les traders ayant des positions courtes qui impliquent des options à la monnaie, près de leur date d’échéance et dans un marché sous-jacent peu volatil, s’exposent ainsi à un fort risque directionnel. Comme ces options sont à la monnaie, leur delta est proche de 50 s’il s’agit de calls ; de -50 s’il s’agit de puts. Mais comme leur gamma est élevé, leur delta peut rapidement passer à 100 s’il s’agit de calls ; à -100 s’il s’agit de puts. Avec un delta de 100 ou de -100, ces positions courtes seraient exposées au risque de voir leur P/L diminuer de près de 100 $ à chaque fois que le sous-jacent évoluerait en leur défaveur.
Pour éviter le risque gamma, il est conseillé de fermer ses positions plusieurs semaines avant l’échéance ; par exemple 21 jours avant l’échéance.
Comment estimer la valeur future d’options à l’aide du gamma
Nous disions en introduction qu’un trader d’options pouvait s’aider du gamma pour estimer la future valeur de son delta, et donc de ses options. Mais comment procéder ? Pour le montrer, nous suivons les explications fournies par Sheldon Natenberg, dans son remarquable ouvrage : Option Volatility and Pricing Advanced Trading Strategies and Techniques.
Prenons le cas d’un call de valeur C, de delta Δ, et de gamma Γ. Quelle serait la nouvelle valeur de ce call si le prix du sous-jacent passait de S1 à S2 ? Pour estimer cette nouvelle valeur, on ne peut pas se contenter de multiplier la différence entre S2 et S1 par le delta initial et d’ajouter ce produit à la valeur initiale C du call. Car le delta est une valeur dynamique : il change en même temps que le prix du sous-jacent. Mieux vaut multiplier la différence entre S2 et S1 par le delta moyen du call. Pour calculer ce delta moyen, on doit d’abord calculer le delta qui serait celui du call si le prix du sous-jacent parvenait à S2 (delta final). On peut utiliser l’addition suivante :
Δ + [(S1 – S2) × Γ]
Pour calculer le delta moyen du call, on divise par deux la somme du delta initial et du delta final à l’aide de cette formule :
Delta moyen = [Δ + Δ + (S1 – S2) × Γ] / 2
On peut maintenant estimer la valeur finale du call en ajoutant à la valeur initiale du call le produit de la différence entre S2 et S1 par le delta moyen :
C + (S1 – S2) × [Δ + (S1 – S2) × Γ/2]
Négocier des options via LYNX
Avec LYNX, vous investissez en options en toute simplicité. Un seul clic de souris vous suffit pour négocier en options sur actions américaines et européennes ainsi qu’en options sur indice. Vous disposez également des meilleurs outils de trading, tels que l’OptionTrader. Et vous pouvez envoyer des combinaisons d’options dans leur intégralité en bourse.
Sources
Natenberg, Sheldon. Option Volatility and Pricing: Advanced Trading Strategies and Techniques, 2nd Edition. New York: McGraw-Hill Education, 2014.


