
Ainsi, la valeur d’une option est déterminée notamment par le cours de la valeur sous-jacente, la durée de l’option jusqu’à son échéance et la volatilité. Mais ces trois variables ne sont pas constantes. La volatilité sur le marché des actions augmente avec l’incertitude, ce qui génère souvent un gonflement de la valeur des options. Les grecques des options permettent de comprendre les changements de la valeur d’une option lorsque les variables changent.
Cet article offre une analyse des différents grecques des options. Pour aller plus loin, le module « OptionTrader » vous permet d’avoir un aperçu des grecques des options sur la plateforme de trading TWS. Si vous cherchez un courtier avec qui trader les options, cliquez ici.
Trading Options
Les grecques des options : des mesures cruciales
Les grecques ne sont peut-être pas le sujet le plus palpitant à discuter, en revanche, elles constituent la base pour bien comprendre la théorie des options. Dans le présent article, nous vous détaillons les principales grecques des options.
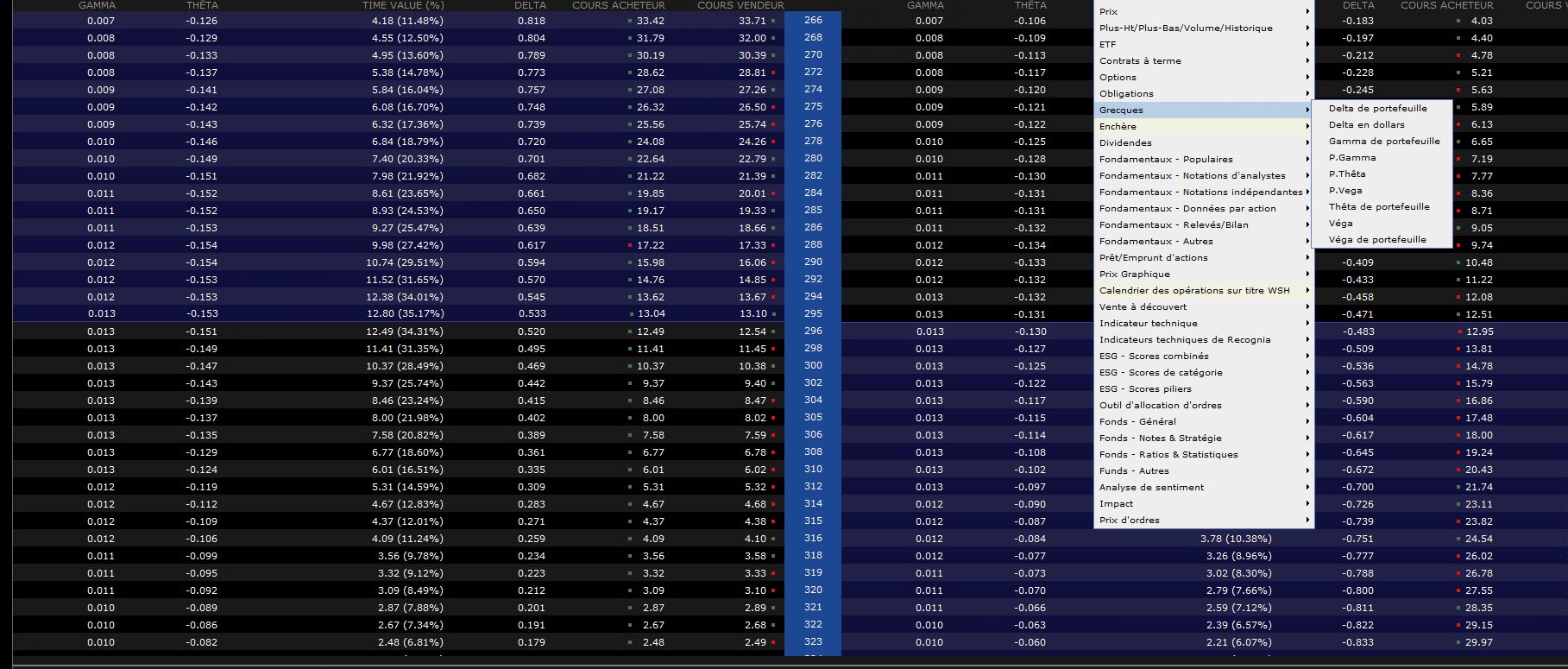
Pour connaître la valeur de la grecque désirée pour l’option désirée, vous pouvez vous rendre dans la chaîne d’options. Dans la plateforme TWS disponible via LYNX, cliquez sur le titre d’une colonne puis sur Insérez une colonne. Dans le menu déroulant qui apparaît, sélectionnez Grecques, puis choisissez la lettre grecque qui vous intéresse (cf. notre image ci-dessus). La chaîne d’options affichera ensuite, pour chaque strike, la valeur correspondante de la grecque choisie.
 Delta
Delta
Le delta est la grecque la plus utilisée. Cette mesure reflète la variation de la valeur d’une option par rapport à la variation du prix de la valeur sous-jacente. Le delta mesure donc l’amplitude de la variation de la valeur d’une option en cas de hausse ou de baisse de l’action sous-jacente. De manière standard, on exprime la variation de valeur qui aurait lieu si le sous-jacente augmentait ou baissait d’un point.
| Prime option call | Delta |
| 2,50 € | 0.50 |
Dans notre exemple, la prime de l’option call correspond à 2,50 € et son delta est égal à 0,5.
Si le prix du sous-jacent augmente de 1 €, alors la valeur de l’option augmente de 0,50 € et passe à 3,00 €.
- Valeur option call 2,50 € ➔ delta 0,50 ➔ valeur option call 3,00 €
Et inversement, si l’action baisse de 1 € alors la valeur de l’option baisse de 0,50 € et passe à 2 €.
- Valeur option call 2,50 € ➔ delta 0,50 ➔ valeur option call 2,00 €
Le fonctionnement du delta pour les options put est identique, sauf que le delta d’un put est toujours négatif (-). Si la valeur sous-jacente baisse de 1 point, alors la valeur du put augmente dans la mesure indiquée par le delta. Si la valeur sous-jacente augmente de 1 point, alors la prime du put baisse dans la mesure indiquée par le delta.
L’équivalent de la probabilité d’une option
Le delta peut également être interprété comme la probabilité qu’une option soit dans la monnaie à son échéance. Il ne s’agit pas d’une approche scientifique mais d’une règle générale qui permet à un adepte des options d’évaluer rapidement la probabilité de voir l’option expirer dans la monnaie.
Imaginez que le delta d’un call est 0,80 (ou -0,80 s’il s’agit d’un put), alors la probabilité que l’option expire dans la monnaie s’élève à 80 %. Si le delta de l’option n’est que de 0,10 alors la probabilité n’est que de 10 %. Un delta de 0,50 correspond à une probabilité d’expirer dans la monnaie de 50 %.
 Gamma
Gamma
En fonction des fluctuations de la valeur sous-jacente d’une option, celle-ci est dite « dans la monnaie », « à la monnaie » ou « en dehors de la monnaie ». Ces fluctuations font évoluer le delta en permanence. Le gamma permet de mesurer la sensibilité du delta. Le gamma mesure la variation du delta qui est engendrée par une variation du cours du sous-jacent. Les options à la monnaie ont le gamma le plus élevé vu qu’une fluctuation de la valeur sous-jacente agit fortement sur le delta de ces options.
Eclaircissement par un exemple
Le tableau ci-dessous reprend le delta et le gamma d’options call expirant dans un mois et prenant pour sous-jacent un indice cotant à 5300 points. Pour simplifier, nous avons arrondi les valeurs gamma.
| Prix d’exercice | Delta | Gamma | Indice + 1 | Nouveau delta |
| 5250. | 0.659 | 0.002 | ➔ | 0.661. |
| 5325 | 0.518 | 0.002 | ➔ | 0.52. |
| 5450 | 0.245 | 0.002 | ➔ | 0.247. |
| 5500 | 0.159 | 0.001 | ➔ | 0.160. |
L’option à la monnaie dont le prix d’exercice est de 5250 a le gamma le plus élevé de 0.02. Si l’indice augmente ou diminue d’un point, alors le delta fluctue de 0.02. Le calcul est simple : vous ajoutez le gamma au delta lorsque l’indice augmente d’1 point ou vous le soustrayez lorsque le sous-jacent baisse d’1 point. Après une augmentation d’1 point, le delta de l’option call 5250 passe donc de 0,659 à 0,661.
Plus la durée d’une option est courte, plus le gamma tend à être élevé. L’explication est assez simple : les options à court terme tendent à avoir une valeur temps inférieure à la valeur temps d’options à plus long terme. Une fluctuation de la valeur sous-jacente peut donc avoir plus d’impact sur la prime d’une option que pour des options à plus long terme.
Par exemple : recherchez le gamma d’une option journalière ou hebdomadaire et vous pourrez constater que celui-ci est bien plus élevé que celui de l’exemple discuté.
 Véga
Véga
La troisième grecque présentée est le véga. Vu que le prix des options varient en fonction de la fluctuation attendue de l’actif sous-jacent, la volatilité joue un rôle important. La volatilité est une mesure des fluctuations des cours du sous-jacent sur une période allant jusqu’à la date d’expiration.
Le véga d’une option exprime la variation de la valeur d’une option par rapport à une variation de la volatilité du sous-jacent. Lorsque la volatilité baisse, cela fait baisser la valeur des options concernées (si les autres variables impactant leur valeur restent constantes). Et à l’inverse, lorsque la volatilité augmente, cela fait augmenter la valeur des options (si les autres variables impactant leur valeur restent constantes).
Le véga et le temps
Le véga varie selon le prix d’exercice et la durée d’une option. Une option à court terme est moins sensible aux changements de la volatilité qu’une option à long terme. Tout comme les autres grecques, le véga est exprimé sous forme de décimales. Il exprime la façon dont évoluerait la valeur d’une option si la volatilité du sous-jacent augmentait ou diminuait d’un point.
Le tableau ci-dessous présente le véga d’options ayant le même sous-jacent mais des dates d’expiration différentes.
| Durée | Prix d’exercice | Volatilité implicite | Véga |
| 24 jours | 5350. | 13,50 % | 5.472 |
| 52 jours | 5350. | 13,60 % | 8.051 |
| 80 jours | 5350. | 13.70 % | 9.985 |
| 206 jours | 5350. | 13.80 % | 16.019 |
En termes absolus, le véga des options de court terme est plus petit que le véga des options de long terme qui ont le même sous-jacent et le même prix d’exercice.
Il est important de savoir que la volatilité prévue pendant la vie d’une option change en permanence. Mais un changement des prévisions à la suite d’un événement soudain tend à impacter davantage les options de court terme.
 Thêta
Thêta
La quatrième et dernière grecque que nous allons examiner est le thêta. Le thêta porte sur l’érosion du temps sur la prime des options.
Mesure de la perte de valeur quotidienne
Lorsqu’une option call hors de la monnaie est achetée, la prime payée pour l’option n’est rien d’autre que la valeur temps. Après tout, les options en hors de la monnaie n’ont pas de valeur intrinsèque. Lorsqu’à la date d’échéance, l’option n’a pas de valeur intrinsèque, alors celle-ci n’est pas exercée et celle-ci expire sans valeur.
À partir du moment de l’achat jusqu’à la date d’échéance, la valeur tend à subir une érosion lente, qui peut s’accélérer avec le temps. Le thêta mesure la perte quotidienne que subirait la valeur d’une option en raison du passage du temps si les autres variables restaient constantes. Plus l’échéance d’une option est proche, plus vite l’option perd de la valeur (si l’option est à la monnaie).
Le tableau ci-dessous présente le thêta d’options à la monnaie ayant le même sous-jacent mais des dates d’expiration différentes.
| Durée | Thêta |
| 24 jours | -1.229. |
| 52 jours | -0.933. |
| 80 jours | -0.775. |
| 206 jours | -0.495. |
Échéances, primes et volatilité
La valeur de l’option qui expire dans 24 jours doit baisser de 1.229 € par jour. Et plus l’échéance se rapproche, plus son thêta augmente. La valeur de l’option qui arrive à échéance dans 206 jours ne doit baisser que de 0,495 € par jour sous l’effet du passage du temps.
Par ailleurs, l’érosion de la valeur temps est un processus qui tend à être constant. Vous auriez tort de croire que la perte en valeur se produit entre la clôture et l’ouverture du prochain jour d’ouverture du marché. Durant la journée, la valeur temps d’une option tend à s’évaporer discrètement.
Le thêta peut également être impacté par le changement de la volatilité. Lorsque la volatilité du sous-jacent augmente, le thêta de l’option concernée tend à augmenter. Lorsque la volatilité du sous-jacent diminue, le thêta tend à diminuer.
Investir dans les options via LYNX
Via LYNX, vous pouvez investir dans les options en toute simplicité. Quelques clics de souris vous suffisent pour négocier des options sur des actions américaines et européennes ainsi que des options sur indice. Vous disposez également des meilleurs outils de trading, tels que l’OptionTrader et vous pouvez envoyer des combinaisons d’options dans leur intégralité en bourse.
